Генерация случайных чисел в javascript.
В javascript часто требуется сгенерировать случайное число. Например, чтобы нарисовать звезду в ночном небе или анимировать хаотические аттракторы. Однако существуют различные способы генерации, и от приложения зависит, какой вы будете использовать.
Базовая генерация
Math.random() всегда возвращает число с плавающей точкой между 0 и 1.
Технически, число, которое вы получите, может быть 0, но никогда не будет точно 1.
Посколько это используется достаточно часто, Math.random() помещают внутрь функции
function getRandom() <
return Math.random();
>
Проблема, конечно, заключается в том, что функция всегда будет создавать случайное число в пределах очень ограниченного диапазона. Большинство других рецептов на этой странице предназначены для того, чтобы решить эту проблему.
Генерация между числами: минимальные и максимальные значения
Чтобы добавить эту функциональность, нам потребуется немного математики.
getRandomInt(10, 20)
> 12
Случайное целое число в диапазоне, включая минимальное и максимальное.
getRandomInRange(1, 10)
> 7
Подбрасывание монеты(случайное true или false)
Если вам нужно получить просто 0 или 1, то используйте следующий код:
function coinToss() <
return Math.floor(Math.random() * 2);
>
coinToss();
> 0
Если нужно конкретно true или false
function coinToss() <
return (Math.floor(Math.random() * 2) === 0);
>
coinToss();
> true
Если вам нужно ассоциировать любые слова со сторонами монеты
Генерация с исключениями
Для ограниченного диапазона целых чисел: создайте массив чисел, которые вы бы хотели вырисовывать, и выберите из него случайное.
var numPool = [ 1, 3, 5, 7, 9, 10 ],
rand = numPool[Math.floor(Math.random() * numPool.length)];
Для чего-нибудь более динамичного: добавьте массив целых чисел, которые вы хотите исключить, и пустой массив, который будет содержать результат фильтрации первого массива во второй.
var numPool = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ];
var excludePool = [ 3, 4 ];
var filteredPool = [];
Затем создайте цикл по массиву numPool, проверьте, есть ли случайное число в массиве исключений excludePool, и поместите результат в массив filteredPool:
Наконец, отобразите случайное число из отфильтрованного массива
var rand = filteredPool[Math.floor(Math.random() * filteredPool.length)];
Генерация случайного, неповторяющегося числа
Для небольших наборов чисел: создайте массив, заполненный элементами, перетасуйте их случайным образом, поместите результат в новый массив, затем достаньте перетасованные элементы один раз:
var numPool = [ 13, 21, 36, 14, 27, 10 ];
function shuffle(numPool) <
for(var j, x, i = numPool.length; i; j = parseInt(Math.random() * i), x = numPool[—i], numPool[i] = numPool[j], numPool[j] = x);
return numPool;
>;
var randomResult = shuffle(numPool);
while( randomResult.length > 0 ) <
console.log( randomResult.pop() );
>
Для более больших наборов чисел: создайте и заполните массив случайными целыми числами, отклоняя любое, которое уже было ранее сгенерировано:
var numReserve = []
while (numReserve.length
В коде выше numReserve заполнен 12 случайными числами между 0 и 1000. Числа затем могут быть получены из массива.
Криптография
Всех показанных выше методов будет недостаточно для создания криптографически защищенных функций. Для этого мы можем использовать Web Cryptography API, создав типизированный массив:
var cryptoStor = new Uint16Array(8);
В этом случае мы создаем массив с 8 различными слотами, каждый из которых может содержать 16-битовое целое число без знака. Другие опции включают Int8Array, Uint8Array, int16Array, Int32Array и Uint32Array.
Теперь заполните массив случайными числами определенного типа
Показаны выбранные значения в консоли:
> [43484, 57947, 46691, 49849, 24272, 11827, 28203, 17423]
Web Cryptography API имеет хорошую поддержку в современных браузерах, хотя в некоторых нужно ставить префиксы.
Копирование материалов разрешается только с указанием автора (Михаил Русаков) и индексируемой прямой ссылкой на сайт (http://myrusakov.ru)!
Добавляйтесь ко мне в друзья ВКонтакте: http://vk.com/myrusakov.
Если Вы хотите дать оценку мне и моей работе, то напишите её в моей группе: http://vk.com/rusakovmy.
Если Вы не хотите пропустить новые материалы на сайте,
то Вы можете подписаться на обновления: Подписаться на обновления
Если у Вас остались какие-либо вопросы, либо у Вас есть желание высказаться по поводу этой статьи, то Вы можете оставить свой комментарий внизу страницы.
Порекомендуйте эту статью друзьям:
Если Вам понравился сайт, то разместите ссылку на него (у себя на сайте, на форуме, в контакте):
Комментарии ( 5 ):
Здравствуйте! Можно вопрос не по теме статьи?
Конечно, можно! Но задайте его, пожалуйста, в службу поддержки: http://support.myrusakov.ru/
Спасибо! В следующий раз, уже ответили на javascript.ru
Прекрасно! Рады за вас!
Для добавления комментариев надо войти в систему.
Если Вы ещё не зарегистрированы на сайте, то сначала зарегистрируйтесь.
Copyright © 2010-2021 Русаков Михаил Юрьевич. Все права защищены.
Способы использования Math.random() в JavaScript
Math.random() — это один из API JavaScript. Это — функция, которая возвращает случайные числа. Диапазон возвращаемых чисел представлен значениями от 0 (включая 0, то есть, она может вернуть 0) до 1 (не включая 1, то есть — единицу она вернуть не может).
Эта функция чрезвычайно полезна при разработке игр, при описании анимаций, при создании наборов данных с использованием метода случайного выбора. Случайные числа применяются в процедуральном искусстве, при создании текстов и во многих других случаях. Эти числа можно использовать в веб-разработке, в мобильной разработке, в обычных настольных приложениях.

Вот пример, размещённый на CodePen, позволяющий генерировать случайные числа в диапазоне от 0 до 1 и от 0 до 10 (включая 0 и 10).
Пример использования Math.random()
Анимация
Вот пример, в котором Math.random() используется для создания анимации.
Музыка, сгенерированная компьютером
Вот проект, демонстрирующий пример использования Math.random() в деле создания компьютерной музыки.
Здесь за основу взята традиционная мелодия «Auld Lang Syne» («Старое доброе время»). Программа строит итоговую композицию, обрабатывая исходный материал по особому алгоритму, основанному на использовании случайных чисел.
Вывод случайного изображения
В данном проекте возможности генератора случайных чисел используются для выбора изображений.
Вывод изображения, выбранного случайным образом
Случайный фоновый цвет
Здесь можно найти проект, в котором показан случайный выбор фонового цвета.
Случайный выбор фонового цвета
Самое интересное происходит в этом фрагменте кода:
Эта функция возвращает случайное целочисленное значение из заданного диапазона. Она используется для настройки характеристик цветов, таких, как тон, насыщенность и светлота.
Если вас интересует вопрос случайного генерирования цветов — взгляните на этот материал.
Процедуральное искусство
Вот проект, в котором случайные числа используются для создания изображения по заданным правилам.
При построении этих необычных кривых функция Math.random() используется дважды. Первый раз — для выбора цветов градиента. Второй раз — для настройки максимального радиуса кривых. Это — прекрасный пример того, как при каждом запуске процесса создания изображения получается что-то новое.
Случайный выбор слов из заранее созданного списка
Здесь можно найти программу, которая выводит на экран слова, случайным образом выбираемые из заранее созданного массива.
Случайный выбор слов
Вот код, который используется для выбора слова:
Этот пример очень похож на тот, где на странице выводится изображение, выбранное случайным образом. Пожалуй, разработка подобной программы хорошо подойдёт новичкам, которые хотят попрактиковаться в работе с веб-технологиями.
Генератор ключей API
Вот проект, в котором случайные числа используются для создания ключей API.
Система для создания случайных ключей API
Это — пример использования генератора случайных чисел, имеющий практическое применение в разработке реальных приложений. Здесь для создания UUID (Universally Unique IDentifier, универсальный уникальный идентификатор) программа генерирует 16 случайных чисел. Такой UUID можно использовать в роли ключа для доступа к некоему API.
Вывод фрагментов текста с использованием переходов, сформированных случайными символами
Здесь можно найти проект, в котором случайные числа используются при выводе текстов.
Переходы между фразами, сформированные с использованием генератора случайных чисел
Игра «Камень, ножницы, бумага»
Здесь можно найти реализацию игры «Камень, ножницы, бумага».
Камень, ножницы, бумага
В этой классической игре Math.random() используется в качестве основы игровой логики. Компьютер делает ход, случайным образом выбирая один из трёх вариантов действий.
Генератор надёжных паролей
Вот программа, представляющая собой генератор надёжных паролей.
Генератор надёжных паролей
Заметки о Math.random()
▍По-настоящему ли случайны числа, которые выдаёт Math.random()?
Они, так сказать, не совсем случайны. Эта функция возвращает псевдослучайные числа. Алгоритм, на котором она основана, называется «генератор псевдослучайных чисел» (Pseudo-Random Number Generator, PRNG). Это значит, что последовательность выдаваемых им чисел может быть, в определённых условиях, воспроизведена.
Случайные числа не случайны
FullStack CTO
FullStack CTO
Как создать генератор случайных чисел на JS и предсказать Math.random()

Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании — напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать.
Генератор псевдослучайных чисел и генератор случайных чисел
Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.
Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.
Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.
Энтропия — это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()
ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ — это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.
Придумываем алгоритм ГПСЧ
Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).
Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:
Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.
А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:
Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9. Кстати, так выглядит распределение по выпадению чисел при 10000 итерациях:
Распределение очень неравномерное, но мы получим генератор чисел от 0 до 9.
Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:
Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random() — это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.
Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них — это Линейный конгруэнтный ГПСЧ(LCPRNG).
Линейный конгруэнтный ГПСЧ
Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
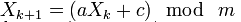
где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:
Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).
Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ — это проблема. Если говорить про другие задачи, то эти свойства — могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.
Еще одно свойство — воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.
Как устроен Math.random()
Как устроен алгоритм Math.random() — интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:
Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.
Исправил ошибку в алгоритме MWC1616 (пропущенные скобки). Эта же ошибка повторяется и в статье https://v8project.blogspot.ru/2015/12/theres-mathrandom-and-then-theres.html
то видим, что должны быть скобки:
Предсказываем Math.random()
Чем это было чревато? Есть такой квест: https://alf.nu/ReturnTrue
Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:
Этот код работал в 70% случаев для Chrome

Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие — числа можно предсказать.
Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.
Новый алгоритм выглядит так:
Сrypto Random Values
Пример генерации случайного числа:
Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).
Материалы про Math.random()
Больше про random в спецификации:
Хорошая статья про работу рандомайзера
Пример реализации предсказателя с Math.random()
Кстати, следить за обновлениями и прочими материалами от меня можно в телеграм канале: @prowebit
Подробно о генераторах случайных и псевдослучайных чисел
Введение
Как отличить случайную последовательность чисел от неслучайной?
Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
Линейный конгруэнтный ГПСЧ (LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений
Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
Вывод данной программы будет примерно таким:
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
Экспоненциальное распределение
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.




